Many real systems (social groups, the brain, economic and transportation networks) display a particular organization of their hubs (nodes with a lot of connections): they are more densely connected among them than expected by chance. In other words, these rich nodes form clubs, called ‘rich clubs’. How do these (structural) rich clubs reflect on dynamical processes taking place on the network? It depends on many aspects: of course, it depends on the dynamics, so here we focus on diffusion dynamics modelled through continuous-time random walks. Then, it also depends on which other types of structures are present in the network, and on their hierarchical relations. In brief: the presence of a strong structural does not imply the existence a strong functional rich club (easier diffusion among rich nodes). The vice versa is also true: functional rich clubs do not translate directly into denser connectivity among hubs. For more detail, and cool plots, see the paper!

In 2017 Manlio De Domenico introduced the family of diffusion distances and induced geometry as a tool for the analysis of the functional organisation of complex networks. Its natural generalisation to multilayer networks was still missing and with this work we filled the gap providing (i) a rigorous mathematical definition of the diffusion distance(s) and induced space(s) in the framework of multilayer networks, (ii) the extension of the diffusion distance definition w.r.t. different random walk dynamics, and (iii) a detailed analysis of the interplay between layer topology, inter-layer connectivity, layer-layer correlations (in terms of edge/partition overlapping), and random walk dynamics.

We introduce in this study CovMulNet19, a comprehensive COVID-19 network containing all available known interactions involving SARS-CoV-2 proteins, interacting-human proteins, diseases and symptoms that are related to these human proteins, and compounds that can potentially target them.

Exchanging information is crucial for many real systems and consequently also assessing the how efficiently a system carries on this task. Here we assume that the pairwise communication efficiency is inversely proportional to their distance (metric on the network). Furthermore, we focus on the efficiency that can be quantified through the topology of and the flows on the network.

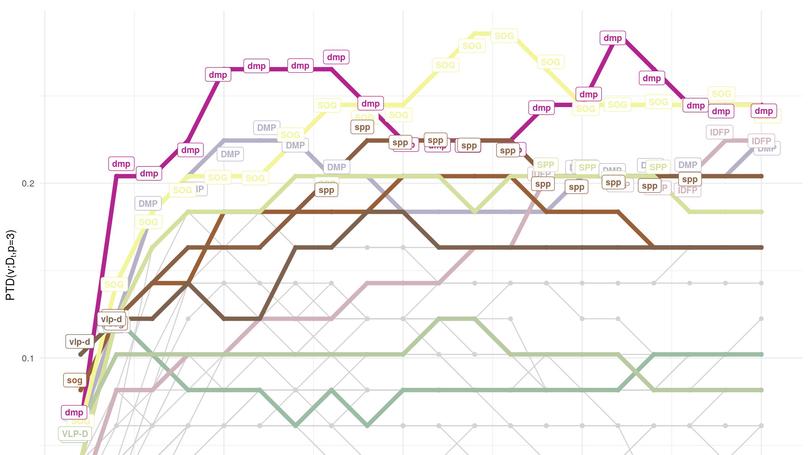
Centrality descriptors are widely used to rank nodes according to specific concept(s) of importance. Despite the large number of centrality measures available nowadays, it is still poorly understood how to identify the node which can be considered as the ‘centre’ of a complex network. In fact, this problem corresponds to finding the median of a complex network. The median is a non-parametric—or better, distribution-free—and robust estimator of the location parameter of a probability distribution. In this work, we present the statistical and most natural generalization of the concept of median to the realm of complex networks, discussing its advantages for defining the centre of the system and percentiles around that centre. To this aim, we introduce a new statistical data depth and we apply it to networks embedded in a geometric space induced by different metrics. The application of our framework to empirical networks allows us to identify central nodes which are socially or biologically relevant.